Impedance of Corroding Metal – Volmer-Heyrovský mechanism
Latest updated: March 24, 2025Introduction – Corrosion series
Corroding systems can show different impedance graphs depending on the nature of the corrosion mechanism. In the first article in this series, we considered a Tafelian system (Part 1) and in this article we will examine a system following the Volmer-Heyrovský mechanism (article 2). You will learn how to express the faradaic impedance and what is the equivalent circuit.
Part II
Let’s study the impedance in the case of anaerobic corrosion of a metal. Following the Volmer Heyrovský corrosion mechanism, valid in deaerated acidic medium, the rate of corrosion depends on the rate of H+ adsorption and H2 release.
How to express the faradaic impedance?
Let’s consider the Volmer-Heyrovsky mechanism:
$\text H^+ + \text s + \text e^- \overset{k_{\text r1}}{\rightarrow} \text{H, s}$ (H adsorption)
$\text H^+ + \text{H, s} + \text e^- \overset{k_{\text r2}}{\rightarrow} \text{H}_2 + \text s$ (H2 release)
Where $\text s$ is an adsorption site and $\text{H, s}$ is a proton adsorbed on the electrode surface.
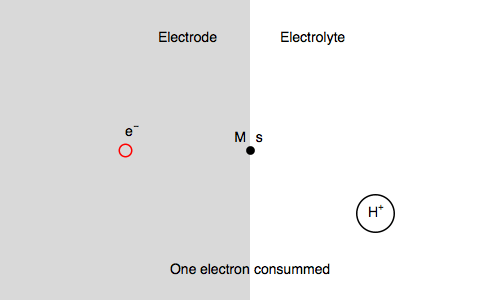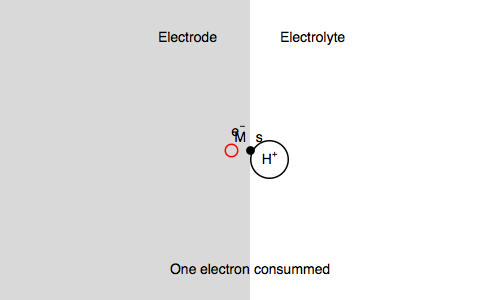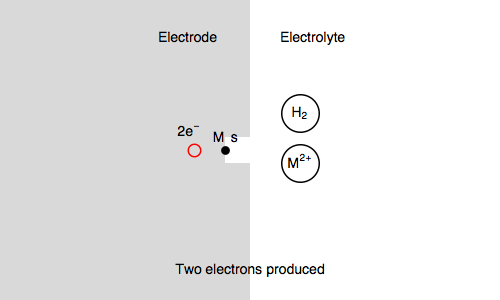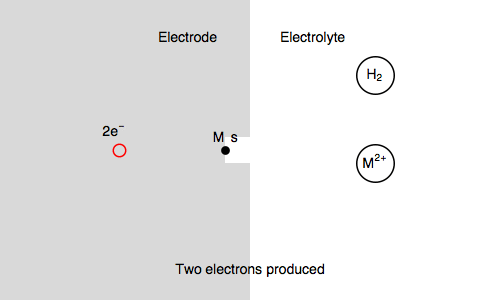
In our case, we also consider $\text{M, s}$ a surface metal atom and the third reaction in the mechanism is:
$\text{M, s} \overset{k_{\text o3}}{\rightarrow} \text{M}^{n+} + n\text e^- + \text s$ (metal corrosion)
The faradaic impedance is expressed by:
$$Z_\text{f} = R_\text{ct} + Z_\text{H} +Z_\text{s}$$
$Z_\text{f} = R_\text{ct} + Z_\theta$ where $Z_\theta= R_\theta/(1+R_\theta C_\theta j 2\pi f)$ is the impedance related to the adsorbed species.
$R_\theta, C_\theta = R_\theta C_\theta (K_{\text r 1},K_{\text r 2})$ for a simple VH mechanism and in our case
$R_\theta, C_\theta = R_\theta C_\theta (K_{\text r 1},K_{\text r 2}, K_{\text o 3})$.
One should note that $R_\theta, C_\theta \lt \text{or} \gt 0$. We will see how this impacts the Nyquist plot.
What is the equivalent circuit?
The equivalent circuit for the faradaic impedance is $R_\text{ct} = R_\theta / C_\theta$ and can be illustrated by the following circuit. Compared to Wagner-Traud (article I), $R_\theta$ and $C_\theta$ are additional components. The ohmic drop is expressed by the resistance $R_\Omega$.
The polarization resistance is $R_\text{p} = R_\text{ct} + R_\theta$.

The Nyquist plot can correspond to a capacitive behavior (top) or an inductive behavior (bottom).
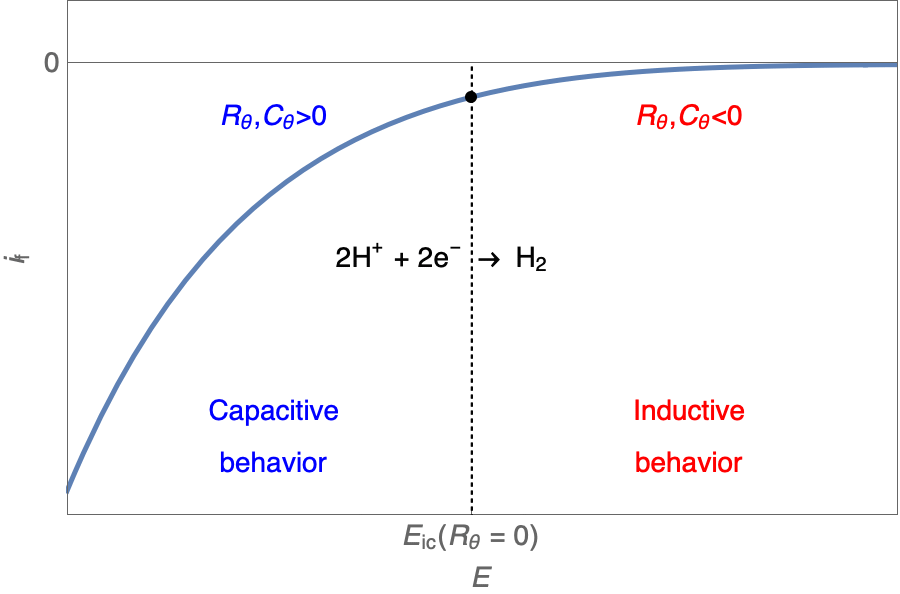
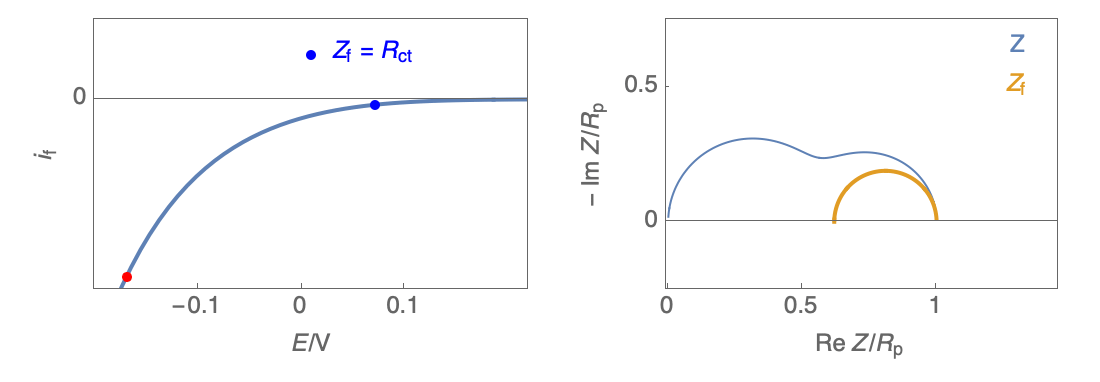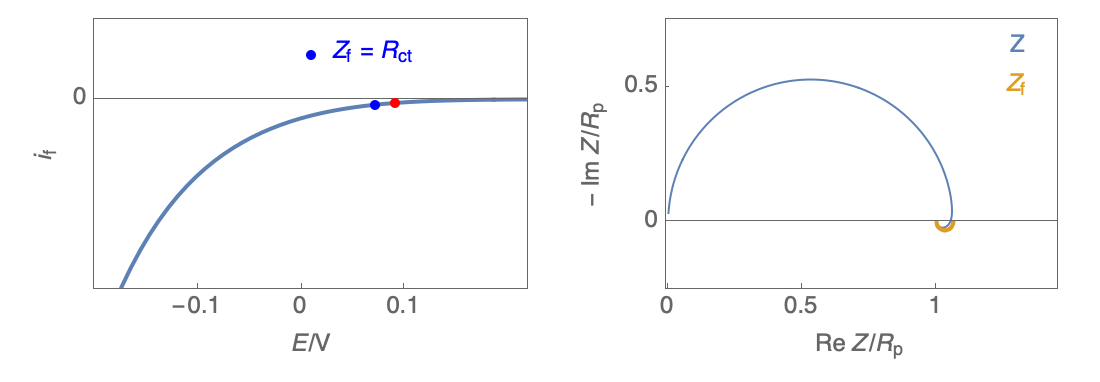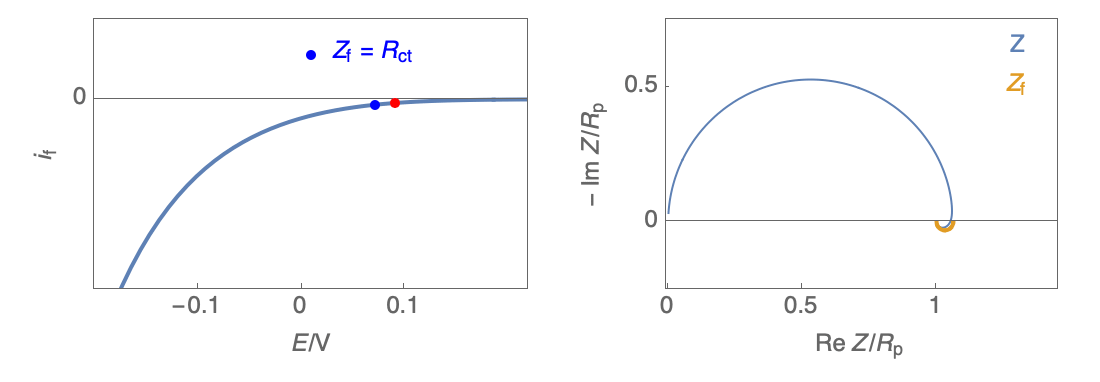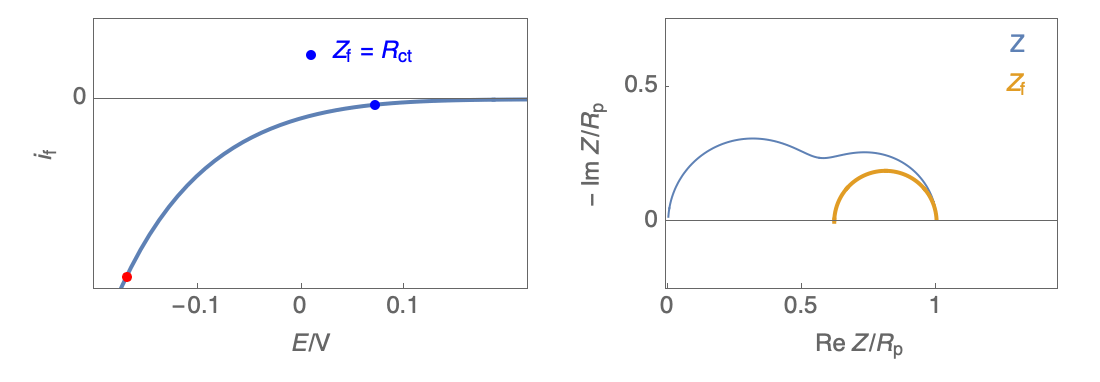
Figure 2: Nyquist plot evolution with the electrode potential for VH mechanism
In the case of $R_\theta, C_\theta \gt 0$, a capacitive behavior can be observed on the Nyquist plot. In the case of $R_\theta, C_\theta \lt 0$, an inductive behavior can be observed. For a potential around $E_\text{corr}$, the Nyquist diagram shows an inductive behavior.
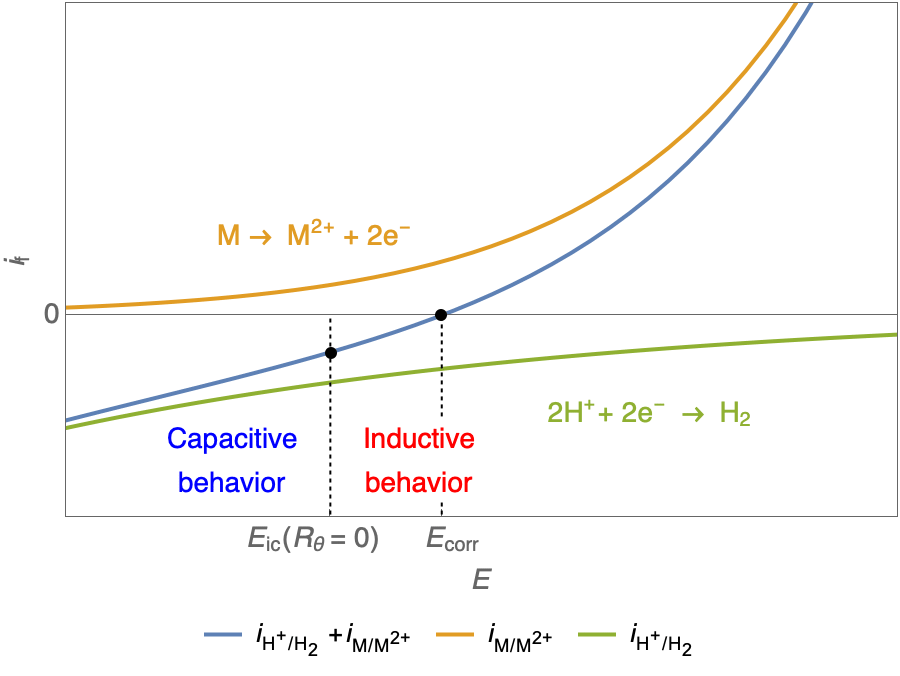
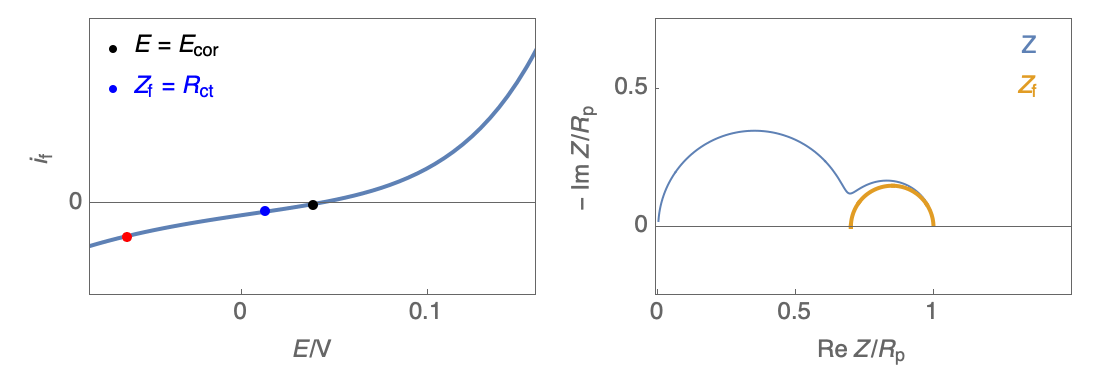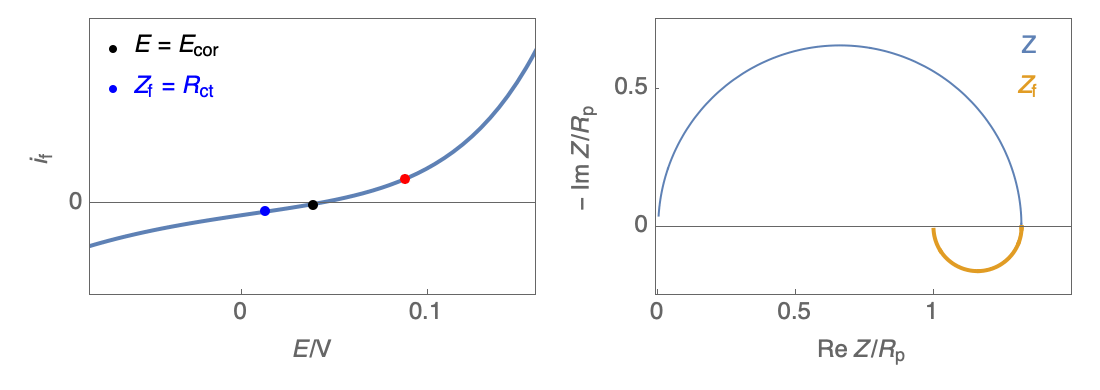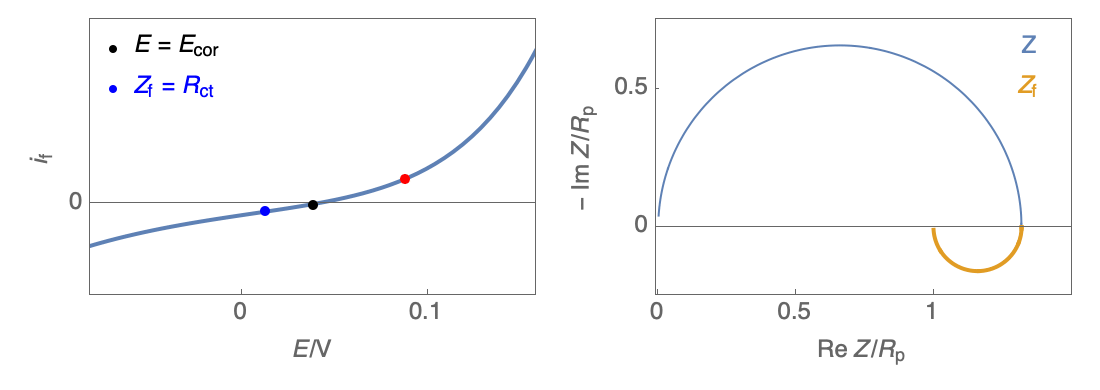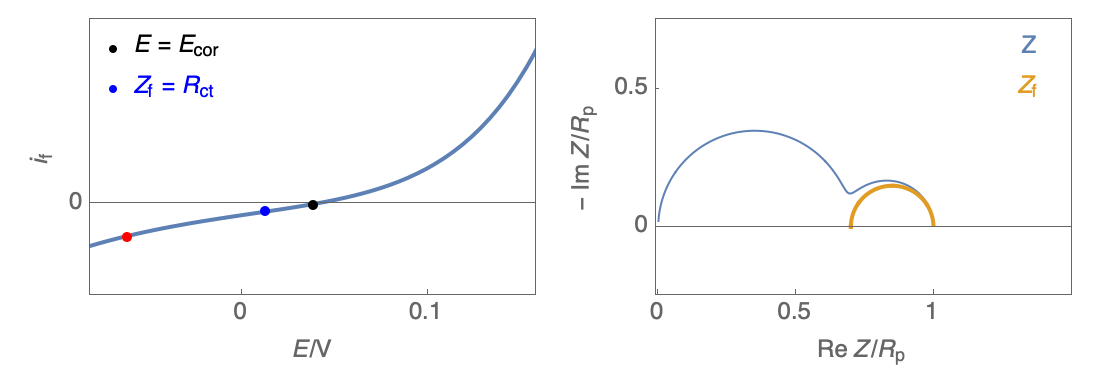
Figure 3: Nyquist plot evolution with the electrode potential for VH corrosion mechanism (bottom)
How to calculate the corrosion current?
In the previous article, we have seen that the Stern – Geary relationship is used to determine the corrosion current and is valid at the corrosion potential:
$$I_\text{corr} = \frac{B}{R_{\text p, E_\text{corr}}}$$
Where $B=b_1b_2/(\text{ln}(10)(b_1 +b_2))$ with $b_{1,2}$ the Tafel slopes, and $R_{\text p, E_\text{corr}}$ the polarization resistance at the corrosion potential.
In our case, the impedance equivalent circuit has an inductive loop at low frequencies, and it does not follow the Wagner-Traud relationship, $R_\text p \neq R_\text{ct}$. So, the Stern-Geary relationship is not valid anymore.
It can be used but an error will be induced if $R_\text p$ is used instead of $R_\text{ct}$.
Conclusion
For a the VH corrosion mechanism, the impedance equivalent circuit is $R_\theta + R_\text{ct} + R_\theta / C_\theta$ and it has an inductive loop at low frequencies. As $R_\text p \neq R_\text{ct}$, the Stern-Geary relationship is not valid anymore. The corrosion current can still be calculated but an error will be induced if $R_\text p$ is used instead of $R_\text{ct}$.





